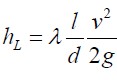|  |
Mindkettő "cricket".
| digitus (ujj) | 0,01848 m | |
| palmus (tányér) | 4 digitus | 0,07394 m |
| pes (láb) | 16 digitus | 0,29574 m |
| cubitus (könyök) | 24 digitus | 0,44361 m |
| gradus (lépés) | 40 digitus | 0,73935 m |
| passus (kettős lépés) | 80 digitus | 1,47870 m |
| pertica (rúd) | 160 digitus | 2,95740 m |
| milia (mérföld) | 8000 digitus | 1478,7 m |
| actus (szakasz) | 12 pertica | 35,5 m |
| négyzetaktusz | 120x120 | 14400 négyszögláb |
| iugerum | 240x120 | 28800 négyszögláb |
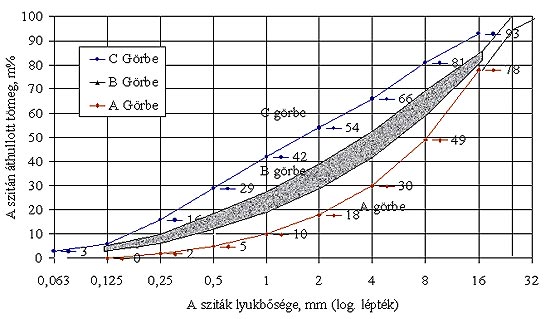
Casagrande készülék:
folyási határ meghatározása
Mielőtt rátérnék a lényegre egy rejtvény a témakörhöz kapcsolódóan:

Megoldás a tovább után.
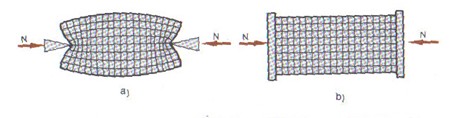
A Saint-Venant-elv kimondja hogy, valamely test vagy szerkezet egy bizonyos szakaszára a működő teher eloszlásának módja lényeges mértékben befolyásolja a teher közvetlen környezetében létrejövő feszültségek és alakváltozások eloszlását, azonban elenyésző hatást gyakorol a távolabbi részek feszültségi és alakváltozási állapotára. Röviden: a teher eloszlásának hatása, csak a teher közvetlen környezetében érvényesül számottevően.


Zsuravszkij-képlet
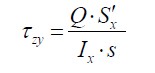
- Q: nyíróerő nagysága
- Sx': az "elcsúszni" akaró rész statikai nyomatéka az x tengelyre
- Ix: az x tengely inercianyomatéka
- s: a keresztmetszet szélessége
A felhajtóerő függ
- A test térfogatától
- A folyadék sűrűségétől
A felhajtóerő nagysága nem függ a test anyagától. Megállapítható hogy a felhajtóerő nem csak folyadékba, hanem gázba merülő testre is ha t.
t.
DEPREZ műszer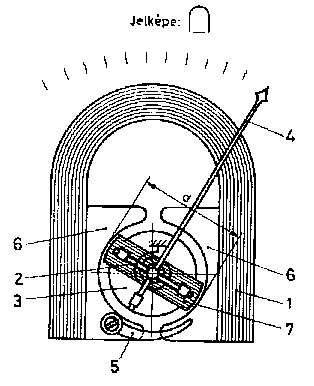
- Állórész – állandó mágnes, melynek erővonalai lágyvason keresztül záródnak
- Lengőrész – tekercs,amely a légrésben helyezkedik el. Ebbe vezetik a mérendő áramot.nÁrambevezetőnek a visszatérítő rugókat használják
- Kitérítő nyomaték – a mágneses térbe elhelyezett árammal átjárt vezetőre ható erő hozza létre

A Thomas-féle Kalkulus a mérnökök matematikai oktatásában világszerte fogalommá vált. Az eredeti, 15 fejezetből álló terjedelmes tankönyv központi témája a differenciál- és az integrálszámítás, célja pedig, hogy az olvasót bevezesse az analízis e két alapvető eszközének legfontosabb alkalmazásaiba. A mű egyik nagy erénye, hogy rendkívül nagy számban tartalmaz kidolgozott példákat, illetve különböző szintű gyakorló-feladatokat, így egységes komplex tankönyvként és példatárként használható. A magyar kiadás 3 kötetben jelenik meg.
Az első kötetet tárgya a differenciálszámítás. Az első fejezet lényegében a továbblépéshez szükséges középiskolai ismeretek összefoglalása. A 2. fejezetben a szerzők a határérték és a folytonosság fogalmát tárgyalják, majd ezt követi a 3. fejezetben a derivált fogalmának bevezetése és a deriválási szabályok ismertetése. A 4. fejezet a derivált legfontosabb alkalmazásait öleli fel, itt kaptak helyet oly fontos és közismert tételek is, mint a Bolzano- vagy a Darboux-tétel.
A második kötet tárgya az integrálszámítás. Mivel a fejezetek folyamatos számozását a 3 kötetben végig fenntartjuk, a 2. kötet az 5. fejezettel indul, melyben a szerzők bevezetik a határozott integrál fogalmát és ismertetik a Newton-Leibniz-tételt. A 6. fejezet a határozott integrál tipikus alkalmazásait tárgyalja, a terület- és térfogatszámítást, továbbá egyes fizikai alkalmazásokat. A 7. fejezet témája a transzcendens függvények. A következő két fejezet ismét az integrál gyakorlati oldalához tér vissza. A 8. fejezetben a különféle integrálási technikákkal ismer-kedhet meg az olvasó, míg a 9. fejezetben az integrál kevésbé triviális alkalmazásairól: a differenciálegyenletek néhány típusáról esik szó.
A 3. kötet a 10. fejezettel kezdődik. A 10. fejezetben a kúpszeletekkel és a polár-koordinátákkal ismerkedhetünk. A 11. fejezet tárgya a véges sorok és sorozatok elmélete. A 12. fejezetbe került a tér koordinátageometriájának ismertetése. A 13. fejezet a vektor értékű függvényekkel és a térbeli mozgások leírásával foglalkozik. A 14. fejezet tárgya a parciális deriváltak, a 15. fejezeté a többszörös integrálok. A 16. fejezet pedig az integrálfogalom kiterjesztésével vektorterekre való foglalkozik.
Az eredeti művet George B. Thomas, a Massachusetts Institute of Technology néhai professzora írta a differenciál- és integrálszámítás oktatására szolgáló tankönyvként.
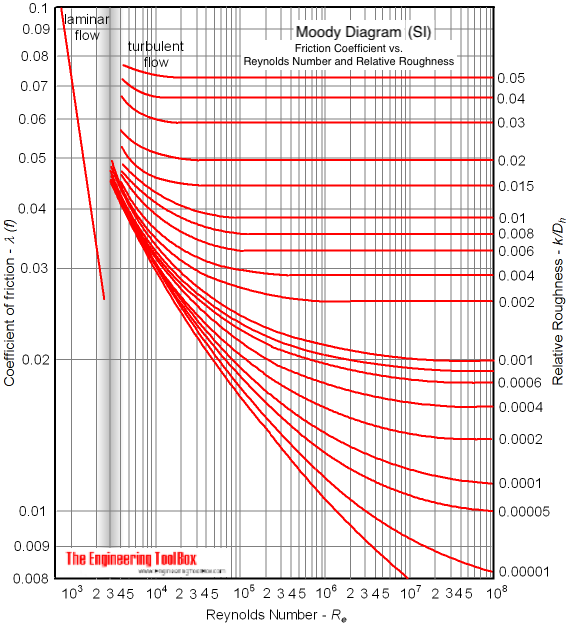
Moody-diagramm a hL veszteségmagasság-számítás csősúrlódási tényezőjére: